Big Bang Contradiction

"Discovery Of A Major Contradiction In Big Bang Cosmology Points To The New Cosmic Center Universe Model"

CERN Preprint, Ext-2003-021 (14 Apr 2003)
by Robert V. Gentry

Abstract

The BAL z = 3.91 quasar's high Fe/O ratio has led to a reexamination of big bang's spacetime expansion postulate and the discovery that it predicts a CBR redshift of z > 36000 instead of the widely accepted z ~ 1000. This result leads an expansion-predicted CBR temperature of only T = 0.08 K, which is contradicted by the experimental T_CBR = 2.73 K. Contrary to long-held belief, these results strongly suggest that the F-L expanding spacetime paradigm, with its expansion redshifts, is not the correct relativistic description of the universe. This conclusion agrees with the earlier finding (gr-qc/9806061) that the universe is relativistically governed by the Einstein static spacetime solution of the field equations, not the F-L solution. Disproof of expansion redshifts removes the only support for the Cosmological Principle, thus showing that the spherical symmetry of the cosmos demanded by the Hubble redshift relation can no longer be attributed to the universe being the same everywhere. The Cosmological Principle is flawed. Instead of the universe being both homogeneous and isotropic, instead it is only isotropic about a nearby universal Center. These results suggest that the new Cosmic Center Universe model, based on Einstein's static spacetime solution of the field equations, deserves the attention of the scientific community. One significant advantage of the new model is that it restores conservation of energy to physics, in stark contrast to the big bang, which involved gargantuan nonconservation of CBR energy losses amounting to more than thirty million times the baryonic mass of the visible universe (gr-qc/9806061).

The observation of a BAL quasar at z = 3.91 with a Fe/O ratio about three times that of the sun [1], contradicts big bang's nucleosynthesis prediction that it should be much less than the sun's in the case of high-z objects. Since this prediction is based on the assumption that the universe is governed by the Friedmann-Lemaitre (F-L) expanding spacetime solution of the Einstein field equations, this discrepancy raises the question as to whether there is a previously undetected flaw in this basic assumption.

We seek the answer by comparing the local Cosmic Blackbody Radiation (CBR) temperature with cosmic expansion's prediction. In theory any CBR photon emitted with standard wavelength, λ_s, has since expanded so as to now exhibit a presently measurable wavelength, λ, given by [2,3],

λ/λs = 1 + z = R / Re,

(1)

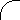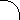where z is the present expansion redshift, and R and R_e are, respectively, the expansion factors at present time, t, and at time of photon emission, t_e. One method of calculating the expansion's present rate of change of λ uses Equation (1) together with MTW's [2] assumption of the temporal constancy of R_e, to obtain (dλ/dt)/λ = λ^⋅/λ = R^⋅/R, or,

λ⋅appx = Hλ = H(1 + z)λs,

(2)

which agrees with the result obtained by Peebles [3]. The subscript in the above appears because Equation (2) is only an approximation due to the fact that it does not account for the temporal variation of R_e. The correct expression for λ^⋅ is obtained from Weinberg's [4] and Peacock's [5] derivation of the exact expression for z^⋅ from Equation (1) by correctly including the temporal variation of R_e, dR_e/dt_e, whereupon,

dz/dt = [Re(dR/dt) − R(dRe/dte)(dte/dt)]/Re2.

(3)

Both Weinberg [4] and Peacock [5] find dt_e/dt = R_e/R, so the foregoing can be rewritten as

z⋅ = [(R/Re)(R⋅/R) − (R⋅e/Re)] = (1 + z)H − He,

(4)

which, except for different notation, is equivalent to Weinberg's Equation 14.6.23, and identical to that obtained in Peacock's Problem 3.2. In both instances their calculations stop with the expression for z^⋅, and neither comment about any unusual implications of Equation (4). Here, however, we continue the calculation to find the exact expression for λ^⋅. To do this we first remember that redshift determinations of distant galaxies are always obtained from Equation (1) on the premise that λ_s represents the exact laboratory standard emission line value corresponding to λ, the present astronomically measured, redshifted wavelength. From this it follows that λ_s is a constant for all times, and hence that Equation (1) leads to z^⋅ = λ^⋅/λ_s. Equating this quantity with the last expression in Equation (4) leads to

λ⋅ = λs[(1 + z)H − He],

(5)

where λ^⋅ represents, as earlier stated, the present rate of wavelength increase of any arbitrary photon that was emitted at H_e = R^⋅_e/R_e, and time, t_e, as measured after the big bang at t = 0. In theory Equation (5) is a prediction that applies to all photons, those arriving from a distant galaxy as well as those in the CBR. For an expanding universe λ^⋅ > 0, and since H ~ t⁻¹ for the various Friedmann models, then all photons presently measured locally must obey the redshift condition, 1 + z > H_e/H = t/t_e. If we let t = t_e + Δt, where Δt is the elapsed time from photon emission to the present, we find

z > Δt/te,

(6)

which is expansion's prediction of the minimum redshift to be expected from the measurement of any arbitrary group of photons emitted with the same standard laboratory wavelength, λ_s, and having a common origin at time t_e. Its unusual implications begin to be evident when it is applied to objects with z > 6. But its most extraordinary implications are even more evident when applying it to redshifts in the early stages of the CBR.

For example, if we apply Equation (6) to the big bang's CBR at time t_e = 1 s, when the radiation temperature of its primordial photons is theorized to be ~ 10¹⁰ K, we find the elapsed time from then to the presumed time of decoupling, when the redshift is theorized [6] to be z = 1089, is only Δt ~ 1000 s, or less than half an hour. This value sharply contradicts the 3.8 × 10⁵ yr value recently reported by Bennett [6].

We can also use Equation (6) to find the expected present value of the CBR temperature by utilizing the most recent estimate [6] of the big bang at t = 13.7 × 10⁹ yr. On that basis Δt ≃ 5 × 10¹⁷ s. Thus it follows that when the dynamic variation of R_e is correctly included into the calculation of expansion's effect on CBR photons, we find the present CBR expansion redshift and the corresponding CBR temperature are predicted to be z_exp > 5 × 10¹⁷ and T_CBR < 2 × 10⁸ K, respectively. Even if we just apply Equation (6) to the usual scenario where the CBR temperature is predicted to be ~ 3000 K at decoupling when t_e = 3.8 × 10⁵ yr [6] we still find predictions of z_exp > 36000 and T_CBR < 0.08 K.

Obviously, both sets of predictions are severely contradicted by the presently observed 2.73 K. Thus, instead of present CBR observations confirming the most important predictions of big bang cosmology, we find they contradict them. It appears there must be a major flaw in big bang's underlying postulate, which is the assumption that the universe is governed by the Friedmann-Lemaitre solution of the field equations. Even more evidence of the very serious nature of this flaw comes from noticing the extraordinary implications of Equation (5). It reveals that the present rate of expansion-induced wavelength change of any photon depends on both the present value of H, and its value at time of emission, H_e. If this were true, then photons in the CBR must have retained a memory of the value of H_e at emission 13.7 × 10⁹ yr ago, and moreover, in some unknown way, must now be able to process that memory on an instantaneous basis in order for Equation (5) to hold. Such a requirement is bizarre. Photons having a memory of the Hubble value at emission is in contradiction to all of modern quantum electrodynamics.

Disproof of expansion redshifts removes the only support for the Cosmological Principle, thus showing that spherical symmetry of the cosmos demanded by the Hubble redshift relation can no longer be attributed to the universe being the same everywhere. The Cosmological Principle is wrong. Instead of the universe being both homogeneous and isotropic, instead it is only isotropic about a nearby universal Center. Thus we find that a new model of the cosmos is needed, one that is not based on the universe being governed by the F-L paradigm, but which is based on observational evidence of a nearby universal Center, and which can also account for the BAL z = 3.91 quasar with its high Fe/O ratio. A new model with these properties has already been developed [7]. It is based on the universe being relativistically governed by the Einstein static spacetime solution of the field equations [8], which is the same relativistic format used to successfully construct the earlier, preliminary version of this model [9,10]. It now deserves the attention of the scientific community because of its ability to account for eight other major predictions of the big bang, but without its spacetime expansion assumption. One significant advantage of the new model is that it restores conservation of energy to physics, in stark contrast to the big bang, which involved gargantuan nonconservation of CBR energy losses amounting to more than thirty million times the baryonic mass of the visible universe [8].

References

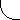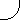1. Hasinger G, Schartel N, and Komassa S, Discovery of an ionized Fe-K edge in the z = 3.91 Broad Absorption Line Quasar APM 08279+5255 with XMM-Newton, 2002 Astrophys. J. 573 L77 [astro-ph/0207005]

2. Misner C W, Thorne K S, and Wheeler J A 1973 Gravitation (New York: W.H. Freeman & Co.) pp 712, 783, 794

3. Peebles P J E 1993 Principles of Physical Cosmology (Princeton University Press) p 95

4. Weinberg S 1972 Gravitation and Cosmology (New York: John Wiley & Sons) pp 416, 451

5. Peacock J A 1999 Cosmological Physics (Cambridge University Press) p 618

6. Bennett C L et. al., First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results, 2003 Preprint astro-ph/0302207

7. Gentry R V, New Cosmic Model Accounts For Eight Of Big Bang's Major Predictions Without Using The F-L Paradigm, 2003 Preprint Submitted to CERN

8. Gentry R V and Gentry D W, The Genuine Cosmic Rosetta, 1998 Preprint gr-qc/9806061

9. Gentry R V, A New Redshift Interpretation, 1997 Mod. Phys. Lett. A 12 2919 [astro-ph/9806280]

10. Gentry R V, The New Redshift Interpretation Armed, 1998 Preprint physics/9810051